【AI学習】必要な数学の基礎をゼロから解説｜統計・線形代数・微積分を学ぶロードマップ

AI学習を進める中で、「もっと深く理解したい」「応用力を高めたい」と感じていませんか？AIの真の力を引き出すためには、数学の基礎知識が不可欠です。

この記事では、AIの根幹を支える統計学、線形代数、微積分の具体的な役割から、数学が苦手な方でも挫折しないための学習ロードマップ、さらにはおすすめの教材まで、AI学習に必要な数学の全てをゼロから丁寧に解説します。

• AI学習における統計学、線形代数、微積分の具体的な役割と重要性
• 各数学分野の基礎概念とAIへの応用例
• 数学が苦手な方でも実践できる効率的な学習ロードマップ
• AI学習におすすめの統計学、線形代数、微積分の教材と学習法

AI学習に数学の基礎が欠かせない理由と主要分野の役割

AIを深く学び、その応用力を高めるためには数学の基礎知識が不可欠です。

数学はAIの動作原理や理論的な背景を理解し、複雑な問題を解決するための強力な思考ツールとなるからです。

AIの理論理解と応用力を高める基盤

AIの理論理解における「基盤」とは、AIのアルゴリズムやモデルが機能する原理を支える根本的な知識のことです。

数学はAIモデルがどのように設計され、どのように学習し、どのように推論を行うのかという、その核心部分を解き明かすための言語を提供します。

例えば、ニューラルネットワークやサポートベクターマシンといったAIモデルは、数式で表現される理論に基づいています。

数学を理解することで、単にライブラリを使ってAIを動かすだけでなく、モデルがなぜ特定の予測をするのか、どのような状況で性能が低下するのかを論理的に分析できるようになります。

これにより、既存のモデルをカスタマイズしたり、新しい課題に合わせて最適なAIを設計したりと、あなたのAI応用力が飛躍的に高まります。

数学は、あなたがAIを「使う」側から「創る」側へ進化するための土台となるのです。

AIモデルの動作原理と性能改善への貢献

AIモデルの「動作原理」とは、AIが入力されたデータを処理し、最終的な出力を生成するまでの内部メカニズムを指します。

この動作原理の深部に数学があります。

例えば、ディープラーニングモデルは、数万から数億ものパラメータを調整しながら学習を進めます。

この調整プロセスには、微積分に基づいた勾配降下法という最適化アルゴリズムが使われます。

モデルが期待通りの結果を出さないとき、数学的な知識があれば、どのパラメータがどのように影響しているのか、どの数式が問題を抱えているのかを詳細に分析できます。

データの特徴を抽出する線形代数や、モデルの予測精度を評価する統計学も同様です。

数学的な理解があることで、単に結果を見るだけでなく、その原因を特定し、より適切なデータ前処理やモデル構造の変更など、具体的な性能改善策を導き出すことが可能になります。

最新AI論文を読み解く力と最先端技術の把握

最新AI「論文を読み解く」力とは、日々進化するAI技術の最先端に触れ、新しい知見や手法を効率的に学習する能力を意味します。

数学は、この能力を養うための必須ツールです。

AI分野は研究開発が活発で、年間で数万本もの論文が発表されています。

これらの論文は、新しいアルゴリズムやモデルの理論を、しばしば数学的な記号や数式（例: シグマ「Σ」、積分記号「∫」）を用いて記述しています。

自然言語処理のTransformerや画像生成のDiffusionモデルといった画期的な技術も、その中核には線形代数や微積分などの数学理論が存在します。

数学の基礎があれば、これらの数式が意味することを正しく解釈でき、提案されている技術の本質や限界を深く理解できます。

これは、AI開発者として常に最新の技術トレンドを追いかけ、自身のスキルを向上させる上で欠かせない能力です。

データサイエンスの基礎を支える統計学の役割

「統計学」とは、データからパターンや傾向を抽出し、未来の事象を予測したり、意思決定を支援したりするための学問です。

AI学習では、データの理解とモデルの評価に欠かせません。

データサイエンスの領域では、日々生成される膨大な量のデータを分析し、そこから有益な知見を引き出すことが求められます。

例えば、AIモデルを訓練するために集めたデータが、本当に偏りのない「良いデータ」であるかを判断するには統計学の知識が必要です。

統計学は、データのばらつきや分布を把握し、外れ値を特定したり、特定の現象が偶然なのか、それとも意味があるのかを評価するための手法を提供します。

モデルが95%の精度で予測したとしても、その数値がどの程度信頼できるのか、異なるデータセットでも同様の結果が得られるのかといった、AIモデルの信頼性や妥当性を客観的に評価する上で、統計的な仮説検定や信頼区間の理解が不可欠です。

AIデータ表現と処理の根幹となる線形代数

「線形代数」とは、ベクトルや行列といった概念を扱い、データの表現、変換、操作の仕組みを数学的に探究する学問分野です。

AIがデータを扱う上での根幹となります。

AI、特に機械学習やディープラーニングの世界では、画像、音声、テキストなどのあらゆる種類のデータが、数値の集合であるベクトルや行列として内部で表現されます。

例えば、1枚のフルカラー画像は、ピクセルごとの色情報を保持する巨大な行列としてAIに認識されます。

AIモデルがこれらのデータを処理する過程では、データの特徴を抽出したり、データを変換したりと、ほぼ全ての計算がベクトルと行列を使った線形演算で行われます。

ニューラルネットワーク内の重み調整や、データから本質的なパターンを見つけるための次元削減なども、線形代数の理論が基盤です。

線形代数を理解することは、AIがデータをどのように「見て」、どのように「理解し」、どのように「操作しているのか」を解明する上で欠かせない知識です。

AIモデルの最適解を導く学習を支える微積分

「微積分」とは、変化する量を解析し、その変化の割合（微分）や累積量（積分）を扱う数学の分野です。

AIモデルが最適な答えを見つける学習プロセスにおいて中心的な役割を担います。

AIモデル、特にディープラーニングは、与えられたデータから「最適解」を見つけるために、損失関数という形で表現される予測誤差を最小化するように学習を進めます。

この最適化の鍵を握るのが微積分です。

例えば、勾配降下法という学習アルゴリズムは、損失関数の「傾き」（勾配）を微分によって計算し、損失が小さくなる方向へモデルのパラメータを少しずつ調整していきます。

これにより、AIは最も適切なパラメータの組み合わせを見つけ出し、精度の高い予測が可能になります。

数多くの変数を同時に考慮してパラメータを調整する際には「偏微分」が、確率分布の計算やモデルの評価には「積分」が使われます。

微積分は、AIモデルがデータから学習し、より良いパフォーマンスを発揮するための根幹となる理論です。

統計学：AI学習を深めるためのデータ理解とモデル評価の基礎

AI学習において、統計学はデータ理解とモデル評価の確かな基盤を提供します。

統計学の知識があれば、単にAIモデルを使うだけでなく、データが持つ意味を深く読み解き、モデルの予測精度や振る舞いを客観的に評価する力が身につくのです。

この理解は、AIの精度向上や問題解決に直結します。

AIにおける不確実性を扱う確率論の基礎

確率論は、AIが扱う「不確実性」を数学的に捉えるための基盤です。

現実世界のデータには常にばらつきや予測不可能な要素があり、AIはその不確実性の中で判断を下します。

例えば、画像認識モデルがある画像を「猫」と90%の確率で認識する場合、この数値の解釈には確率論の理解が不可欠です。

モデルの信頼性や確信度を理解し、誤認識のリスクを評価するために使われます。

概念	AIにおける役割	具体例
確率分布	データ発生のパターン表現	異常検知、画像認識のカテゴリ分類の出力
ベイズの定理	不確実な情報からの推論	スパムメールの判定、医療診断の確信度算出
期待値	長期的な平均的な結果予測	モデルの損失関数の最適化、強化学習の報酬最大化

確率論の知識は、AIモデルが持つ不確実性を適切に評価し、現実世界の問題へ応用する上での重要な思考基盤となります。

データ特徴を把握する記述統計の活用

記述統計は、大量のAI学習データが持つ特徴を数値やグラフで要約し、一目で把握できる形にするための手法です。

これにより、データの前処理や特徴量エンジニアリングの段階で、データの偏りや異常値を素早く見つけ出せます。

例えば、あるデータセットの年齢分布を調べる場合、平均年齢が35歳、標準偏差が10歳だと分かれば、データの中心やばらつき具合を即座に理解できます。

このような情報は、AIモデルの性能に影響を与えるデータの特性を深く知るために不可欠です。

指標	意味	AI学習データでの活用
平均値	データの代表的な中心	特徴量の標準化、欠損値の補完
中央値	外れ値に影響されにくい中心	給与データなど、偏りがある場合の代表値把握
分散・標準偏差	データのばらつき度合い	特徴量のスケール確認、データ分布の把握
歪度・尖度	データ分布の形	異常値の特定、正規分布からの乖離度評価
相関係数	変数間の関係性の強さと方向性	特徴量間の多重共線性の検出、有用な特徴量の選定

記述統計は、AIモデルに投入する前のデータを「読み解く力」を養い、適切な前処理やモデル選択を行うための土台となります。

モデル予測精度を評価する推測統計の重要性

推測統計は、AIモデルが学習した限られたデータから、まだ見ていないデータや将来の事象について推論するための統計学です。

AIモデルの予測が単なる偶然ではないか、汎用性があるかを科学的に検証する上で極めて重要です。

例えば、新しいAIモデルを開発した際、そのモデルが既存モデルよりも本当に優れているのかを評価するために、統計的仮説検定を用いることがあります。

これにより、新しいモデルが改善したという結果が、たまたまの誤差ではなく、統計的に意味のある違いであるかを判断できます。

評価手法	AIにおける役割	具体例
仮説検定	モデル間の性能差の統計的有意性検証	新しいアルゴリズムと既存の精度の比較、A/Bテストでの効果検証
区間推定	モデル予測の信頼度範囲の評価	予測された株価の範囲、ユーザー行動予測の精度信頼区間算出
回帰分析	複数変数と結果の関係性解析	広告効果の要因分析、顧客満足度予測の要因特定
分散分析	複数グループ間の平均値差の検証	異なる学習設定によるモデル性能の違い分析、グループごとの効果比較

推測統計を理解することは、AIモデルの予測能力を客観的に評価し、信頼できるAIシステムを構築するために欠かせない要素です。

統計学の効率的な学習範囲と学習法

AI学習における統計学は、「どの範囲まで深く学ぶべきか」という疑問を持つ人が多くいます。

効率的に学習を進めるためには、AIの目的と照らし合わせて必要な範囲を見極めることが肝要です。

私自身の経験では、まず「記述統計」と「確率論の基礎」を固め、その後「推測統計」の応用へと進むと、途中で挫折しにくいと感じます。

それぞれの分野で、単に公式を覚えるだけでなく、その意味するところやAIのどのような場面で活用されるのかを意識しながら学習を進めることが重要です。

学習ステップ	内容	重点と理由
ステップ1	記述統計の基礎（平均、分散、中央値など）	データの全体像を把握し、前処理や特徴量エンジニアリングの基礎知識となるため
ステップ2	確率論の基礎（確率分布、ベイズの定理など）	AIモデルの不確実性や推論の原理を理解するために必須なため
ステップ3	推測統計の基礎（仮説検定、区間推定など）	AIモデルの性能評価や汎用性の検証に必要な知識となるため
ステップ4	実装を通じた応用（Pythonなど）	理論を実際のAI開発に活かす実践力を養うため

AI学習における統計学は、はじめから全てを網羅しようとせず、基本的な概念を「なぜそれが重要なのか」という視点で理解を深め、段階的に応用力を高めていく方法が最も効率的です。

AI学習におすすめの統計学教材とオンライン講座

AI学習に役立つ統計学の教材やオンライン講座は数多くありますが、私から特におすすめするのは、理論だけでなく実践も重視したコンテンツです。

数学が苦手な方でも、実際のコードやデータに触れながら学べるものを選ぶと、理解が深まります。

具体的な例としては、Pythonを使ったデータ分析の基礎から学べるUdemyの講座や、直感的な解説で統計の概念を教えてくれる書籍が学習に役立ちます。

教材の種類	特徴	おすすめポイント
オンライン講座（Udemy）	講義動画と演習を通じて実践的に学べる	Pythonなどのプログラミング言語と連携しながら、統計学の知識をAIに応用する方法を習得できる
専門書籍（例: 統計学入門）	体系的な知識をじっくり深掘りする	理論的背景を網羅的に学習でき、AI論文の理解にもつながる
プログラミング学習サイト	短い演習を通して基本概念を身につける	コーディングしながらの学習で、すぐに実践に役立つスキルを磨ける

AI学習における統計学の知識を身につけるには、自分に合った学習スタイルで継続できる教材を選ぶことが成功への鍵となります。

線形代数：AIがデータを処理する土台となる表現と計算の要点

AIが膨大なデータを正確に理解し、高度な処理を行うためには、線形代数という数学分野の理解が不可欠です。

線形代数は、データ表現の基本からAIモデル内部の複雑な計算まで、AIシステムを構築する上での基盤となります。

要素	AIにおける役割	学習するメリット
ベクトル・行列	データを数値として表現する基本形式	画像やテキストなどのデータ構造を把握
行列演算	AIモデル内部のデータ変換・処理を実行	ニューラルネットワークの計算原理を理解
固有値・固有ベクトル	データの特徴を抽出し、効率化に応用	次元削減やデータ解析の基礎を習得

AIが学習を進め、賢明な判断を下すための土台を、線形代数が提供します。

線形代数を学ぶことで、AIの「データ処理」の核心を理解できるでしょう。

AIデータ表現の基本となるベクトルと行列

AIにおいて、「ベクトル」は方向と大きさを持つ量を示す数学的実体、「行列」はこれらのベクトルを縦横に並べたデータ構造を指します。

現実世界の複雑な情報である画像、テキスト、音声などは、AIに理解させるために最終的にこれらの数値データとして表現されます。

例えば、100ピクセル×100ピクセルのモノクロ画像であれば、各ピクセルの明るさの値を並べた10,000次元のベクトルとして表現できます。

カラー画像では、赤・緑・青の各色チャネルに対して同じようにベクトルが作られ、それらが重ねられた行列になります。

テキストデータも、単語の出現頻度や意味的な関係性を数値化したベクトル（単語埋め込み）として表現され、複数の単語ベクトルを並べて行列として扱います。

概念	AIデータ表現での役割	具体例
ベクトル	単一のデータ要素を数値列で表現	画像のピクセル値、単語埋め込みの数値
行列	複数のデータ要素や特徴量をまとめて表現	画像の集合、文章の単語ベクトル群

データを行列やベクトルで表現することは、AIがデータを数値的に処理し、パターンを認識するための出発点となるのです。

AIモデル内部の変換を担う行列演算の理解

AIモデル内部で行われる複雑な計算のほとんどは、「行列演算」、つまり行列同士の足し算、引き算、掛け算といった操作で構成されています。

特に、行列の積はニューラルネットワークにおける情報の伝達や変換の核心を担います。

ニューラルネットワークの各層では、入力されたデータベクトルが重みと呼ばれる行列と掛け合わされ、次の層へ伝達されます。

たとえば、隠れ層が3つあるニューラルネットワークでは、最初の入力データ（ベクトル）に一つ目の重み行列が乗算され、その結果が二つ目の重み行列に乗算される、というようにデータが次々と変換されます。

このような一連の行列演算により、AIモデルは入力データから様々な特徴を抽出し、最終的な出力（分類結果や予測値など）を生成しているのです。

演算の種類	AIモデルでの活用例	具体的な場面
行列の積	ニューラルネットワークの情報伝達と変換	複数の入力特徴量から新たな特徴量を作成する重み付け計算
転置行列	データの次元合わせ、相関係数の計算	データ分析における特徴量間の関係性の把握

行列演算の理解は、AIモデルがデータをどのように変換し、最終的な結果を導き出すのかという、内部の動作原理を深く理解するために欠かせません。

データの特徴抽出に応用される固有値・固有ベクトル

線形代数における「固有値」は、行列がベクトルを変換する際に、そのベクトルの「伸び縮み率」を示すスカラー値、「固有ベクトル」はその伸び縮みする「方向」を示すベクトルです。

これらは、データの中からその特徴を最もよく表す重要な方向を見つけ出す際に活用されます。

代表的な応用例は、次元削減手法の主成分分析（PCA）です。

例えば、100個の異なる特徴量を持つデータセットがあったとします。

PCAは、このデータセットが持つ情報量の大部分を失うことなく、より少ない5つの「主成分」（固有ベクトルに対応）でデータを表現することを目指します。

これにより、データのノイズを減らし、AIモデルの学習効率を向上させることが可能です。

概念	AIデータ分析での役割	具体的な応用例
固有値	データ変換における変動の大きさを示す	主成分分析（PCA）でのデータ分散の測定
固有ベクトル	データ変換における軸（方向）を示す	PCAでのデータの主要な特徴軸の特定

固有値と固有ベクトルを理解することは、膨大なデータの中から真に意味のある特徴を見つけ出し、AIモデルの精度向上や処理の効率化に貢献するために極めて重要です。

線形代数の効率的な学習範囲と学習法

AI学習における線形代数の効率的な学習では、抽象的な証明よりも、概念の理解と具体的な計算、そしてAIへの応用例に焦点を当てることが重要です。

まずは基礎概念から段階的に学び、プログラミングで実践を繰り返すことが鍵になります。

具体的な学習範囲としては、以下の項目を押さえてください。

• ベクトルと行列の基本概念: ベクトル、行列の定義、基本的な演算（和、差、スカラー倍）。
• 行列の積: 最も重要な演算であり、ニューラルネットワークの基盤を理解するために必須です。
• 行列式と逆行列: 連立一次方程式の解法や線形変換の性質を理解するために必要です。
• 線形空間と基底: データの次元や変換の自由度を把握する土台となります。
• 固有値と固有ベクトル: 主成分分析などの次元削減技術への応用を意識した理解です。

学習方法としては、最初に基本的な定義や公式を理解し、例題を通して実際に手を動かして計算してみることをお勧めします。

次に、PythonのNumPyライブラリを使って、学んだ線形代数の概念をプログラミングで再現する演習を20回程度行うことで、理論と実践を結びつけられます。

AI学習におすすめの線形代数教材とオンライン講座

AI学習を進める上で、線形代数の知識は不可欠です。

自身の現在の数学レベルや学習スタイルに合わせた適切な教材やオンライン講座を選ぶことが、学習を成功に導く鍵となります。

教材を選ぶ際には、数式が羅列されているものよりも、図解が多く、具体例やPythonなどのプログラミングを用いた実践例が豊富に掲載されているものを選ぶと良いでしょう。

また、完全に独学で進めるのが難しいと感じる場合は、専門講師から直接指導を受けられるオンライン講座を活用することも効果的です。

タイプ	教材名（例）	おすすめポイント
書籍（入門）	『やさしく学べる線形代数』（石村園子）	イラストが豊富で初心者でも理解しやすい
書籍（実践）	『Pythonによるあたらしい線形代数の教科書』（三宅良昌）	プログラミングと線形代数を結びつけ、実践力が身につく
オンライン講座	Udemy「AIのための線形代数基礎」	動画で視覚的に学べ、演習問題で定着度を高める
オンライン講座	Coursera「Mathematics for Machine Learning」	MITやImperial College Londonが提供、網羅性が高い

これらの教材や講座を活用し、地道に学習を積み重ねることで、AIを深く理解するための線形代数の基礎力を着実に養うことができます。

微積分：AIモデルの学習を支える最適化の鍵となる理論と実践

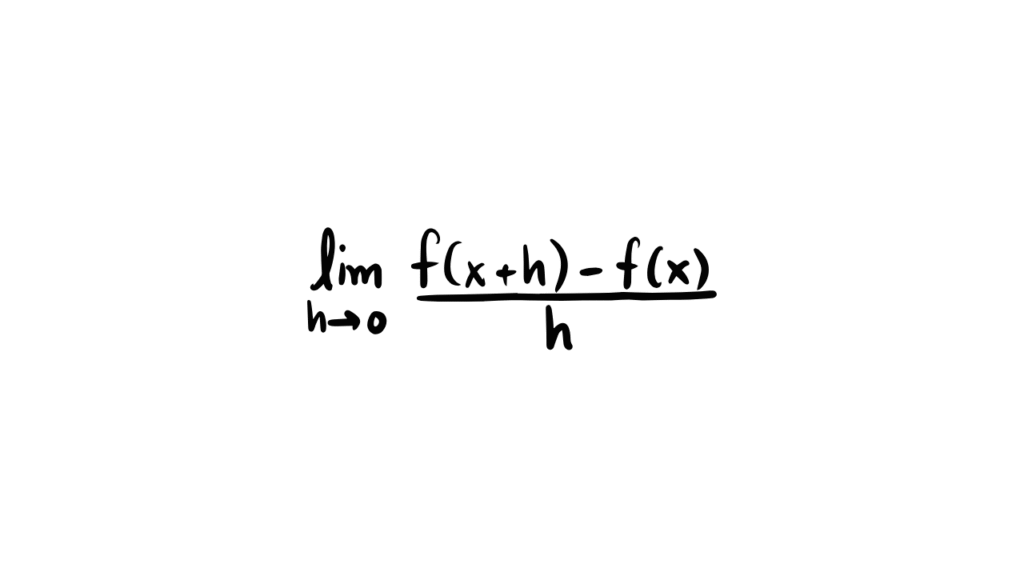
AIモデルの性能向上には、その学習と最適化が不可欠です。

微積分は、AIモデルがデータから学び、最適な予測や分類を行うための「最適な解」を見つけ出すプロセスを支える、中心的な役割を果たします。

微積分の知識を習得することで、AIモデルがどのように機能し、どのような改善の余地があるのかを深く理解できます。

AIモデル最適化の核となる微分の役割

微分は、AIモデルが最も効率的に学習し、最適な性能を発揮するために不可欠な数学的手法です。

特に、AIが予測誤差を最小化しながら学習を進める際に利用する勾配降下法と呼ばれる最適化アルゴリズムの中核を担います。

AIモデルには、数万から数億ものパラメータが含まれることがあります。

微分は、これらの各パラメータがどの方向に、どれくらいの大きさで変化すれば、AIモデルの予測精度が最大になるかを示します。

AIは、この微分の計算結果である「勾配」に基づいて、パラメータを少しずつ調整し、繰り返し学習を進めていくのです。

微分は、AIモデルがデータから学び、精度を高めていくプロセスを可能にする根幹の技術です。

複数変数を調整する偏微分の応用

偏微分は、複数の要素が絡み合うAIモデルの学習において、特定の要素だけを変化させたときに、モデルの出力がどのように変わるかを把握する手法です。

これは、AIモデルが多くの入力情報（変数）を同時に扱う際に特に重要になります。

AIモデルの学習においては、膨大な数のパラメータを同時に、かつ独立して調整する必要があります。

例えば、画像認識モデルでは、約100万ピクセルを超える画像データに対し、それぞれのピクセル値や色情報、適用するフィルター係数といった個別のパラメータがAIモデルの学習に与える影響を、偏微分で評価し最適化しています。

偏微分によって、複雑なAIモデルの効率的な学習が可能になり、より高精度な予測や分類が実現できるのです。

確率密度関数計算を支える積分の基礎

積分は、AIモデルにおける確率的な挙動を理解し、その信頼性を評価する上で重要な役割を果たします。

特に、AIが直面する不確実性を数学的に表現する確率密度関数や、モデルの予測誤差を示す損失関数の計算に利用されます。

AIモデルの学習において、予測結果が特定の範囲内に収まる確率を求める際、積分の概念が用いられます。

例えば、顔認識AIが多数の画像から人物を特定する際に、認識の確信度を確率分布として捉え、その正確な範囲を積分で計算できます。

この計算によって、AIモデルの予測の信頼性や不確実性の度合いを定量的に評価できます。

積分は、AIモデルが「不確実性」を扱い、「総合的な性能」を理解するために不可欠な、基盤となる数学的ツールです。

微積分の効率的な学習範囲と学習法

AI学習を効率的に進めるためには、微積分のどこまで学ぶべきか、そしてどのように学ぶべきかを理解することが重要です。

基礎的な概念であれば、集中して取り組めば数週間程度で把握できます。

重要なのは、AIがどのように動作しているかという全体像の中で微積分を捉える視点です。

項目	内容
学習範囲	微分の定義、勾配の計算、極値の求め方、偏微分、積分の基本的な考え方、確率密度関数との関係性
学習法	概念の図解による理解、実際のAI応用例の把握、プログラミングでの実装演習

微積分の学習は、単なる知識習得に留まらず、AIの問題解決能力を向上させる実践的なスキルとなるでしょう。

AI学習におすすめの微積分教材とオンライン講座

AI学習に役立つ微積分の教材とオンライン講座は、多岐にわたります。

初心者から一歩踏み込みたい方まで、目的別に3つの学習リソースを紹介します。

専門用語に圧倒されずに、着実に理解を深めるための教材選びが肝心です。

種類	教材/講座名	特徴
オンライン講座	Udemy「AI数学入門」	AIに必要な数学をゼロから解説し、微分、積分、線形代数、統計学を網羅。Pythonでの実装演習も含まれる内容
書籍	斎藤康毅著「ゼロから作るDeep Learning」シリーズ	ディープラーニングの原理をPythonコードと数式で基礎から丁寧に解説。微積分の具体的な応用例を多数掲載
書籍	高等学校 数学III 参考書	微積分の基礎概念を網羅的に学べる内容で、体系的な知識を復習したい場合に有用

これらのリソースを活用し、自身の学習スタイルに合わせた進め方で、AI学習の基盤となる微積分の知識を確実に身につけてください。

数学が苦手でも大丈夫！AI学習を成功へ導く学習ロードマップと実践のコツ

AI学習において数学は不可欠な要素ですが、苦手意識がある人でも心配いりません。

適切な学習ロードマップと実践のコツを掴めば、誰でもAI開発に役立つ数学の知識を身につけられます。

ここでは、AI学習を成功へ導く具体的なステップと、モチベーションを維持する秘訣を解説します。

基礎概念を理解する最初のステップ

まず、数学の基礎を学ぶ際に重要なのは、数式そのものよりも用語と概念を直感的に理解することです。

複雑な計算手順を覚えるよりも、その概念が何を表し、AIのどの部分に応用されるのかを把握することに集中しましょう。

例えば、線形代数では「ベクトルとは何か」「行列の積が何を意味するのか」といった基本的な操作のイメージを掴むと理解が深まります。

最初から完璧を目指すのではなく、AI学習に欠かせない統計学、線形代数、微積分それぞれの基本原理をざっくりと捉えることから始めるのが良い学習法です。

学んだ数学を実践で活かすプログラミング演習

学んだ数学の知識は、プログラミングを通して実際に動かすことで、より深く定着します。

AIに必要な数学理論をインプットした後は、簡単なPythonコードやオープンソースのライブラリを使って、実際に手を動かす演習に取り組んでみましょう。

例えば、微分を学んだ後に簡単なPythonコードで勾配降下法を実装すると、理論が現実の世界でどのように機能するかを体験できます。

自分でコードを書いて結果を確認すると、数式だけでは得られない直感的な理解と納得感を得られます。

実践を通して知識を深掘りする継続学習

一度学んだ知識は、継続的に実践と結びつけることで、さらに深く応用力を高めます。

AI学習のプロセスで疑問点が生じたら、その都度関連する数学の知識を深掘りすることが有効です。

AIの最新論文では、新しい数学的概念や既存の理論の応用が頻繁に登場します。

具体的なAIモデルを開発する中で、「なぜこのアルゴリズムがこの数式を使うのか」「この結果を改善するにはどの数学的要素を調整すべきか」といった疑問が生じた際に必要な数学を都度学習すると効果的です。

継続的な実践は、AIエンジニアやデータサイエンティストとしての専門知識を強化します。

学習モチベーションを維持する楽しさの体感

AI学習を続ける上で、学んだ数学がAIの仕組みを解き明かす楽しさを体感することは非常に重要です。

具体的な成果を出すことで、モチベーションは大きく向上します。

例えば、自分で実装したAIモデルが、例えば画像認識で90%以上の精度を出すと、数学がその成功にどれだけ貢献しているかを実感できます。

AI開発において数学的知識を活かし、問題を解決できたときの達成感は、次の学習への大きな原動力となります。

技術コミュニティに参加し、仲間と学びを共有することも、楽しさを維持する秘訣です。

初心者向けおすすめオンライン講座と書籍

数学の基礎からAI学習に活かせる知識まで、効率的に学べる質の高いオンライン講座や書籍を選びましょう。

数多くの選択肢の中から、自身の学習スタイルや目標に合った教材を見つけることが、成功への鍵となります。

教材名	特徴	おすすめポイント
Udemy「AI数学入門」	AI学習に必要な統計学、線形代数、微積分を網羅的に解説	数学が苦手な人でも視覚的な解説で理解を深められる
ゼロから作るDeep Learning（斎藤康毅著）	Pythonでニューラルネットワークを実装しながら学べる	実践的なコードと共にディープラーニングの数学的背景を体系的に理解できる
統計学入門（東京大学出版会）	統計学の基礎から応用まで詳細に解説	統計学の理論を体系的に深く学習する基礎的な書籍
Coursera「Mathematics for Machine Learning」	インペリアル・カレッジ・ロンドン提供の専門講座	機械学習に必要な線形代数と多変数微積分の基礎を実践的に学ぶ

これらの教材は、数学の基礎を固めながらAI学習を円滑に進めるための強力なサポートとなります。

よくある質問（FAQ）

まとめ

AI学習の真の力を引き出すために、数学的思考力を養うことが不可欠であるという点に焦点を当て、統計学、線形代数、微積分それぞれの役割、具体的な応用例、そして効率的な学習法までを詳細に解説しました。

この記事を通して、以下の重要なポイントを理解していただけたでしょう。

• AIの理論を深く理解し、モデルの動作原理を解明する上で必須の統計学、線形代数、微積分それぞれの働き
• 数学に苦手意識がある方でも、段階的に学習を進め、実際にコードを動かすことで応用力を高めるロードマップ
• 継続的な学習を支え、モチベーションを維持するための実践的なアプローチと最適な教材
• AI開発やデータサイエンスの分野で自信を持って活躍するための具体的な指針

本記事で示した学習の道筋と実践のヒントを参考に、AI学習に必要な数学の基礎を着実に身につけて、あなたのキャリアをさらに発展させていきましょう。